Možná vám to s těmi neuronovými sítěmi není pořád moc jasné. Tak si to ukážeme na příkladu, dosti jednoduchém. Mějme matici 2x2 body a snažme se pomocí neuronové sítě identifikovat, zda je v matici nakreslený znak / nebo \ - tedy normální a zpětné lomítko. Ponechme samozřejmě stranou, že na tuto úlohu je neuronová síť kanon na vrabce, k tomu si řekneme něco na závěr…
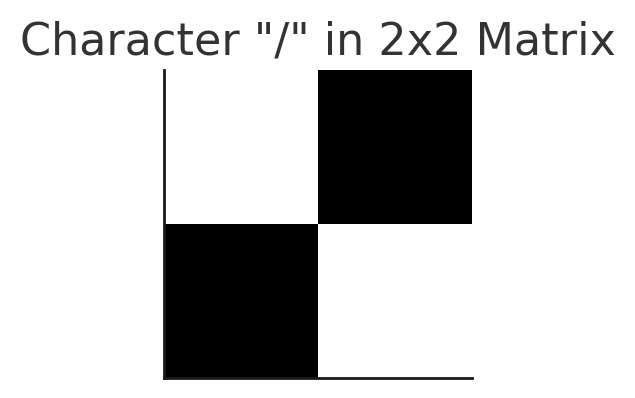
Tento obrázek znaku “/” v matici 2x2 body ilustruje, jak jsou hodnoty 0 a 1 použity k reprezentaci znaku a jak je tedy použijeme k tokenizaci:
- Hodnota 1 označuje černý pixel.
- Hodnota 0 označuje bílý pixel.
Ve výsledné matici zápis vypadá takto.
[0, 1]
[1, 0]
Nyní ho převedeme na jednorozměrné pole, čili dáme řádky za sebe: [1, 0, 0, 1].
Nyní máme tedy vstupní data reprezentovaná čtveřicí čísel a tato data pošleme do neuronové sítě. Tu jsme si navrhli následovně:
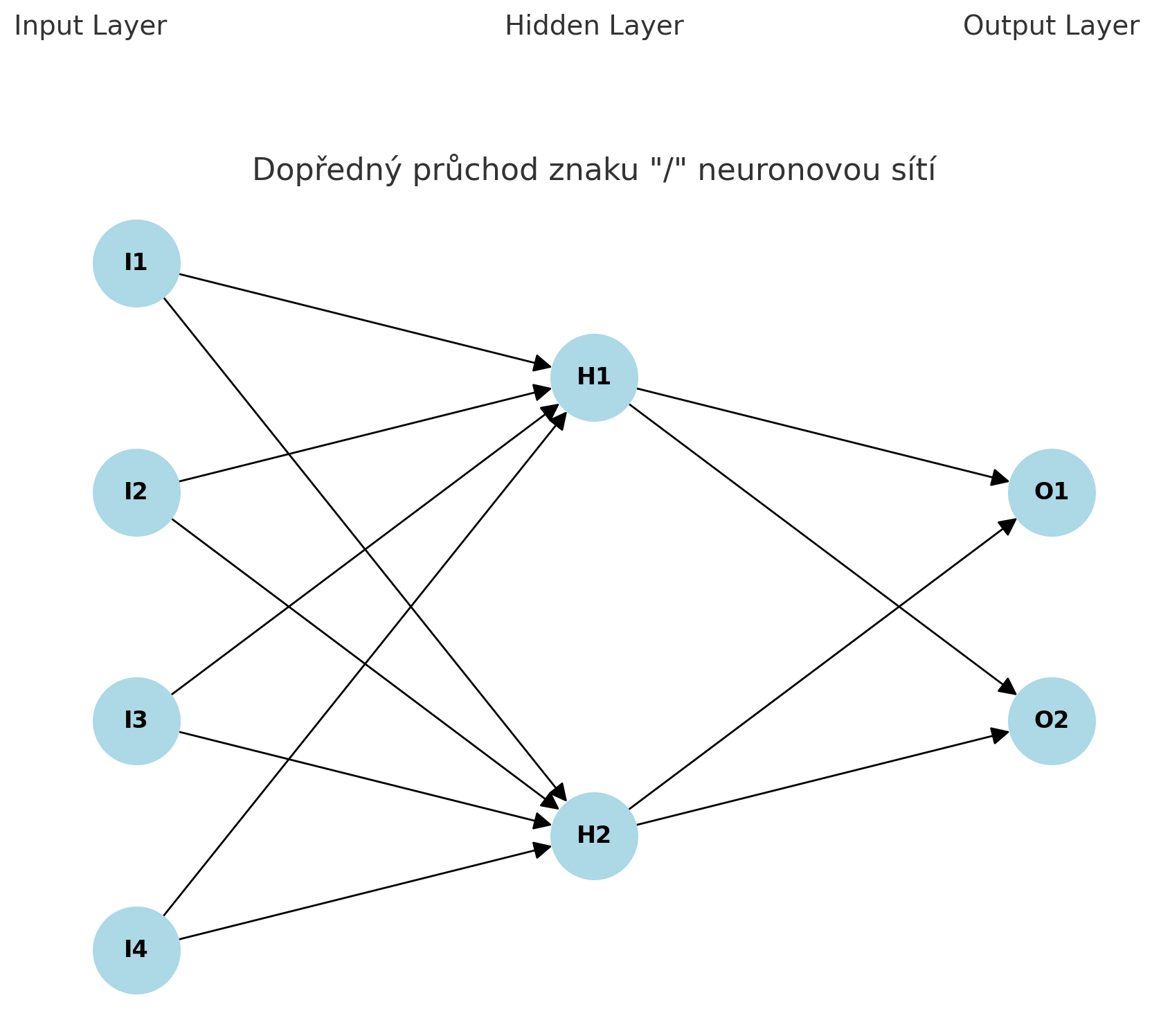
1. Vstupní vrstva:
- Neurony I1, I2, I3, I4 reprezentují jednotlivé pixely matice 2x2, tedy máme čtyři vstupní neurony.
- Pro znak “/” má vstupní pole hodnoty
[0, 1, 1, 0]- to tedy pouštíme do neuronky v prvním vstupu.
2. Skrytá vrstva:
- Neurony H1 a H2 přijímají vstupy od všech čtyř neuronů z vstupní vrstvy.
- Váhy a biasy určují, jak se tyto vstupy kombinují.
3. Výstupní vrstva:
- Neurony O1 a O2 přijímají vstupy od neuronů H1 a H2.
- Neuron O1 může reprezentovat pravděpodobnost, že znak je “/”, a neuron O2 pravděpodobnost, že znak je “\”.
Proč jsme použili dva neurony ve skryté vrstvě? V neuronových sítích, zejména v těch s více vrstvami (deep neural networks), jsou skryté vrstvy klíčové pro schopnost sítě učit se složité vzory a reprezentace. Počet neuronů ve skryté vrstvě je důležitým faktorem, který ovlivňuje výkonnost sítě. V tomto konkrétním příkladu jsme použili dva neurony ve skryté vrstvě, aby byla ilustrace jednoduchá a přehledná, a zároveň aby bylo možné zachytit více informací z vstupních dat. Odpovídá to dvěma očekávaným možnostem vstupu :)
V dalším kroku provedeme Dopředný průchod přes skrytou vrstvu. Každé číslo z neuronu označeného I dorazí do neuronu označeného H po směru šipek. A na každém neuronu je provedena s přicházejícím číslem matematická operace, takzvaná aktivace. Každý neuron ve skryté vrstvě přijímá vstupy od všech 4 neuronů ve vstupní vrstvě. Pro jednoduchost uvážíme následující náhodně inicializované váhy a biasy:
Neuron 1 ve skryté vrstvě:
- Váhy: W_1 = [0.2, -0.3, 0.4, 0.1]
- Bias: b_1 = 0.1
Neuron 2 ve skryté vrstvě:
- Váhy: W_2 = [-0.1, 0.5, -0.4, 0.2]
- Bias: b_2 = -0.2
Bias (česky Posun) je parametr v neuronové síti, který se přidává k váženému součtu vstupů před aplikací aktivační funkce. Bias umožňuje modelu lépe přizpůsobit se datům a zajišťuje, že neurony mohou modelovat posun dat od počátku osy (originu). Bias funguje podobně jako absolutní člen v lineární rovnici. V neuronové síti pomáhá posunout aktivační funkci neuronu nahoru nebo dolů, což umožňuje lepší modelování dat. Bias se přidává k váženému součtu vstupů, což umožňuje neuronu aktivovat se, i když jsou všechny vstupy nulové.
Váhy (weights) jsou klíčovými parametry v neuronové síti, které určují sílu spojení mezi jednotlivými neurony. Váhy násobí vstupní signály před tím, než se tyto signály sečtou a přidá se k nim bias. Poté se výsledek přenese k aktivační funkci neuronu. Váhy určují, jak silně každý vstupní signál ovlivňuje výstup neuronu.
Kontrolní otázka: kde se vzala tato čísla pro Váhy a Bias? Zvolili jsme je náhodně. V reálných aplikacích se váhy inicializují náhodně a pak se optimalizují během procesu tréninku neuronové sítě, kdy bychom vzali v úvahu kýžený výsledek, tedy někdo by v rámci dat zaznačil, která matice je který znak. Neuronová síť by následně procesem učení byla schopna stanovit optimální Váhy a Bias tak, aby mohla být matice a tím i znak správně rozpoznán.
Nyní si spočítejme aktivaci pro první neuron pro znak / - tedy výsledek, který dostaneme na H1. Jako aktivační funkci použijeme ReLU z toho důvodu, že se pro tento typ dat hodí, správný výběr aktivační funkce je nicméně důležitý a je součástí vašeho budoucího know-how, jak optimalizovat neuronovou síť…
z_1 = (0 * 0.2) + (1 * -0.3) + (1 * 0.4) + (0 * 0.1) + 0.1
z_1 = 0 + (-0.3) + 0.4 + 0 + 0.1
z_1 = 0.2
a_1 = ReLU(z_1) = max(0, z_1)
a_1 = max(0, 0.2)
a_1 = 0.2
A teď si spočítejme aktivaci pro druhý neuron pro znak / - tedy výsledek, který dostaneme na H2.
z_2 = (0 * -0.1) + (1 * 0.5) + (1 * -0.4) + (0 * 0.2) - 0.2
z_2 = 0 + 0.5 + (-0.4) + 0 - 0.2
z_2 = -0.1
a_2 = ReLU(z_2) = max(0, z_2)
a_2 = max(0, -0.1)
a_2 = 0
V dalším kroku se posouváme do výstupní vrstvy, provádíme takzvaný Dopředný průchod přes výstupní vrstvu:
Každý neuron ve výstupní vrstvě přijímá vstupy od všech 2 neuronů ve skryté vrstvě. Pro jednoduchost uvážíme následující váhy a biasy:
Neuron 1 ve výstupní vrstvě (pro znak “/”):
- Váhy: W_{output1} = [0.3, -0.5]
- Bias: b_{output1} = 0.1
Neuron 2 ve výstupní vrstvě (pro znak “/”):
- Váhy: W_{output2} = [-0.2, 0.4]
- Bias: b_{output2} = -0.1
Výpočet aktivace pro první neuron ve výstupní vrstvě:
z_{output1} = (0.2 * 0.3) + (0 * -0.5) + 0.1
z_{output1} = 0.06 + 0 + 0.1
z_{output1} = 0.16
z_{output2} = (0.2 * -0.2) + (0 * 0.4) - 0.1
z_{output2} = -0.04 + 0 - 0.1
z_{output2} = -0.14
Nyní aplikujeme funkci softmax na výstup obou neuronů ve výstupní vrstvě. V našem příkladu, kde rozpoznáváme znaky “/” a “\”, je softmax vhodná, protože nám umožňuje interpretovat výstupy neuronů jako pravděpodobnosti jednotlivých tříd (znaků). Bylo by možné použít i jiné funkce jako Sigmoid nebo Tanh, ale ty nejsou pro tento typ úlohy tak vhodné. Nebojte, praxí se naučíte volit, která aktivační funkce je zde nejvhodnější…
A nyní prakticky, jak aplikace softmaxu vypadá.
softmax(z)_i = exp(z_i) / sum(exp(z_j) for j in range(2))
Provedeme tedy výpočet dosazením hodnot, omlouvám se za nepřehlednost, ale teprve se učím LaTex formát zápisu matematiky, snad si poradíte. My si ukážeme výpočet jen pro znak lomítka / - tedy to, jak dorazil na O1 a O2.
exp(0.16) = 1.1735
exp(-0.14) = 0.8694
sum = 1.1735 + 0.8694 = 2.0429
softmax(0.16) = 1.1735 / 2.0429 = 0.574
softmax(-0.14) = 0.8694 / 2.0429 = 0.426
Výstupy softmax funkce jsou tedy: [0.574, 0.426]
Tady si to ještě ukážeme graficky pro vstup znaku / do neuronky s našimi váhami a biasem:
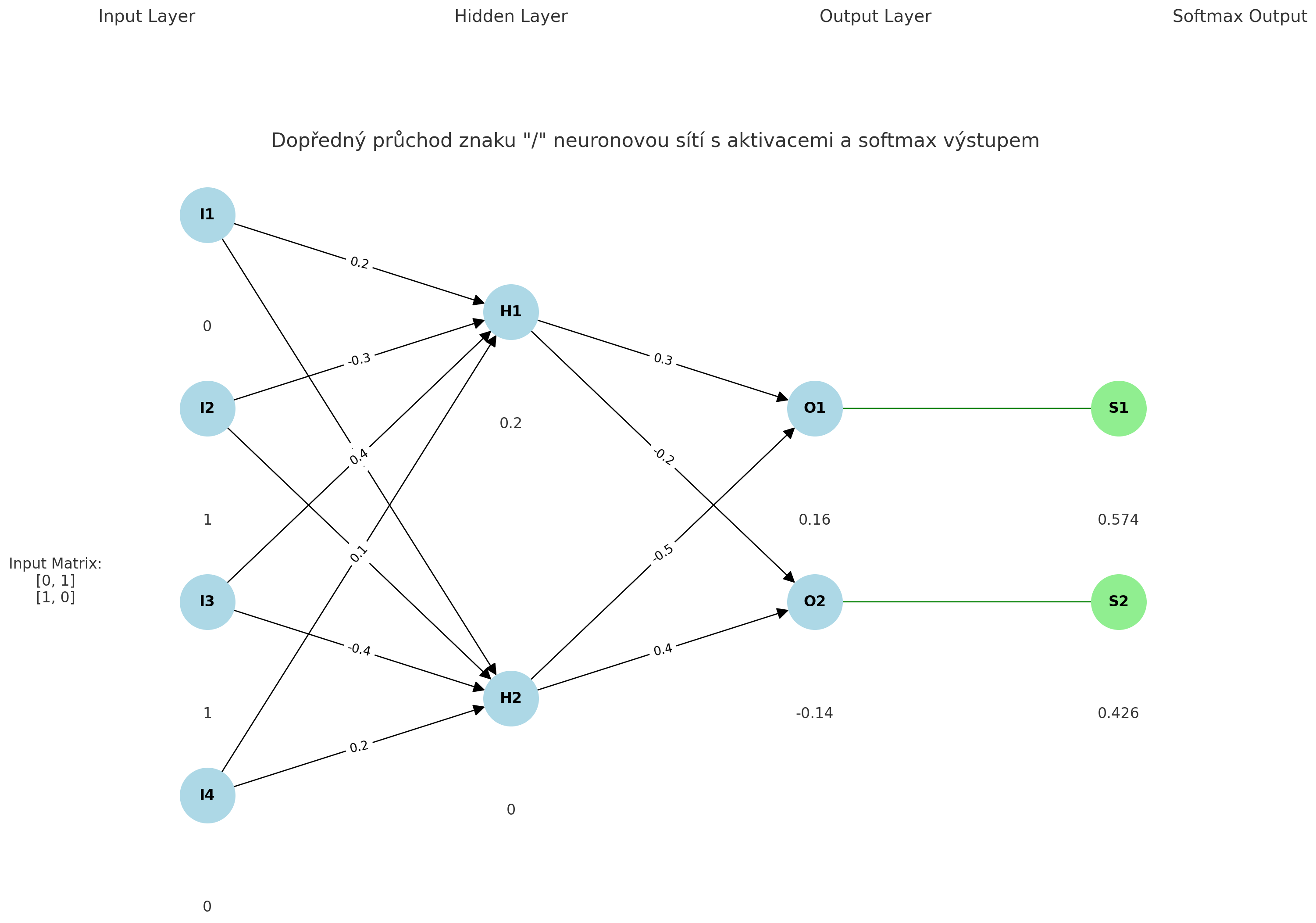
Shrnutí
Pro znak “/” nám vyšly pravděpodobnosti: [0.574, 0.426] - tedy s pravděpodobností 57,4 % se jedná o znak lomítka.
Pro znak “\” si je můžete výsledky dopočítat sami. Kontrola by neměla být těžká :)
Tak a už jsme doma. Neuronová síť usoudila s pravděpodobností 57,4 %, že znak “/” je znakem lomítka. Jak to, že to vyšlo, když jsem říkal, že záleží na hodnotách? Inu proto,že jsem váhy a bias vybral rozumně tak, aby to vyšlo a ne tak, aby hned první, co uvidíte, byla neuronka, která usoudila blbost, i když za to nemůže. Jak jsme si ale řekli, záleží zejména na váhách (A pak taky dobře zvolené aktivační funkci), že neuronka všechno správně rozpozná. A právě tohle je ten fine-tuning. Jen pro pořádek, znak zpětného lomítka jsme rozpoznali s pravděpodobností 59,9 % - taky to není špatné.
Výpočty ukazují, jak softmax funkce převádí surové skóre na pravděpodobnosti, které umožňují interpretovat výstupy neuronové sítě jako pravděpodobnosti pro různé třídy. Bez tréninku mohou být tyto hodnoty náhodné, protože váhy a biasy nejsou optimalizovány.
Snad to bylo pochopitelné!
A co s tím víc? Inu, přidat to učení :)

 |
|  | flashlights, headlamps Fenix & outdoor | Vybavení do přírody
| flashlights, headlamps Fenix & outdoor | Vybavení do přírody